С ними находятся внутри логарифмов.
Примеры:
\(\log_3x≥\log_39\)
\(\log_3 {(x^2-3)}< \log_3{(2x)}\)
\(\log_{x+1}{(x^2+3x-7)}>2\)
\(\lg^2{(x+1)}+10≤11 \lg{(x+1)}\)
Как решать логарифмические неравенства:
Любое логарифмическое неравенство нужно стремиться привести к виду \(\log_a{f(x)} ˅ \log_a{g(x)}\) (символ \(˅\) означает любой из ). Такой вид позволяет избавиться от логарифмов и их оснований, сделав переход к неравенству выражений под логарифмами, то есть к виду \(f(x) ˅ g(x)\).
Но при выполнении этого перехода есть одна очень важная тонкость:
\(-\) если - число и оно больше 1 - знак неравенства при переходе остается прежним,
\(-\) если основание - число большее 0, но меньшее 1 (лежит между нулем и единицей), то знак неравенства должен меняться на противоположный, т.е.
|
\(\log_2{(8-x)}<1\) Решение: |
\(\log\)\(_{0,5}\)
\((2x-4)\)≥\(\log\)\(_{0,5}\)
\({(x+1)}\) Решение: |
Очень важно! В любом неравенстве переход от вида \(\log_a{f(x)} ˅ \log_a{g(x)}\) к сравнению выражений под логарифмами можно делать только если:
Пример . Решить неравенство: \(\log\)\(≤-1\)
Решение:
|
\(\log\)\(_{\frac{1}{3}}{\frac{3x-2}{2x-3}}\) \(≤-1\) |
Выпишем ОДЗ. |
|
ОДЗ: \(\frac{3x-2}{2x-3}\)
\(>0\) |
|
|
\(\frac{3x-2-3(2x-3)}{2x-3}\) \(≥\) \(0\) |
Раскрываем скобки, приводим . |
|
\(\frac{-3x+7}{2x-3}\) \(≥\) \(0\) |
Умножаем неравенство на \(-1\), не забыв при этом перевернуть знак сравнения. |
|
\(\frac{3x-7}{2x-3}\) \(≤\) \(0\) |
|
|
\(\frac{3(x-\frac{7}{3})}{2(x-\frac{3}{2})}\) \(≤\) \(0\) |
Построим числовую ось и отметим на ней точки \(\frac{7}{3}\)
и \(\frac{3}{2}\)
. Обратите внимание, точка из знаменателя – выколота, несмотря на то, что неравенство нестрогое. Дело в том, что эта точка не будет решением, так как при подстановке в неравенство приведет нас к делению на ноль. |
|
|
Теперь на ту же числовую ось наносим ОДЗ и записываем в ответ тот промежуток, который попадает в ОДЗ. |
|
|
Записываем окончательный ответ. |
Пример . Решить неравенство: \(\log^2_3x-\log_3x-2>0\)
Решение:
|
\(\log^2_3x-\log_3x-2>0\) |
Выпишем ОДЗ. |
|
ОДЗ: \(x>0\) |
Приступим к решению. |
|
Решение: \(\log^2_3x-\log_3x-2>0\) |
Перед нами типичное квадратно-логарифмическое неравенство. Делаем . |
|
\(t=\log_3x\) |
Раскладываем левую часть неравенства на . |
|
\(D=1+8=9\) |
|
|
Теперь нужно вернуться к исходной переменной – иксу. Для этого перейдем к , имеющей такое же решение, и сделаем обратную замену. |
|
|
\(\left[ \begin{gathered} t>2 \\ t<-1 \end{gathered} \right.\) \(\Leftrightarrow\) \(\left[ \begin{gathered} \log_3x>2 \\ \log_3x<-1 \end{gathered} \right.\) |
Преобразовываем \(2=\log_39\), \(-1=\log_3\frac{1}{3}\). |
|
\(\left[ \begin{gathered} \log_3x>\log_39 \\ \log_3x<\log_3\frac{1}{3} \end{gathered} \right.\) |
Делаем переход к сравнению аргументов. Основания у логарифмов больше \(1\), поэтому знак неравенств не меняется. |
|
\(\left[ \begin{gathered} x>9 \\ x<\frac{1}{3} \end{gathered} \right.\) |
Соединим решение неравенства и ОДЗ на одном рисунке. |
|
|
Запишем ответ. |
Среди всего многообразия логарифмических неравенств отдельно изучают неравенства с переменным основанием. Они решаются по специальной формуле, которую почему-то редко рассказывают в школе:
log k (x ) f (x ) ∨ log k (x ) g (x ) ⇒ (f (x ) − g (x )) · (k (x ) − 1) ∨ 0
Вместо галки «∨» можно поставить любой знак неравенства: больше или меньше. Главное, чтобы в обоих неравенствах знаки были одинаковыми.
Так мы избавляемся от логарифмов и сводим задачу к рациональному неравенству. Последнее решается намного проще, но при отбрасывании логарифмов могут возникнуть лишние корни. Чтобы их отсечь, достаточно найти область допустимых значений. Если вы забыли ОДЗ логарифма, настоятельно рекомендую повторить - см. «Что такое логарифм ».
Все, что связано с областью допустимых значений, надо выписать и решить отдельно:
f (x ) > 0; g (x ) > 0; k (x ) > 0; k (x ) ≠ 1.
Эти четыре неравенства составляют систему и должны выполняться одновременно. Когда область допустимых значений найдена, остается пересечь ее с решением рационального неравенства - и ответ готов.
Задача. Решите неравенство:
Для начала выпишем ОДЗ логарифма:
Первые два неравенства выполняются автоматически, а последнее придется расписать. Поскольку квадрат числа равен нулю тогда и только тогда, когда само число равно нулю, имеем:
x
2 + 1 ≠ 1;
x
2 ≠ 0;
x
≠ 0.
Получается, что ОДЗ логарифма - все числа, кроме нуля: x ∈ (−∞ 0)∪(0; +∞). Теперь решаем основное неравенство:

Выполняем переход от логарифмического неравенства к рациональному. В исходном неравенстве стоит знак «меньше», значит полученное неравенство тоже должно быть со знаком «меньше». Имеем:
(10 − (x
2 + 1)) · (x
2 + 1 − 1) < 0;
(9 − x
2) · x
2 < 0;
(3 − x
) · (3 + x
) · x
2 < 0.
Нули этого выражения: x = 3; x = −3; x = 0. Причем x = 0 - корень второй кратности, значит при переходе через него знак функции не меняется. Имеем:

Получаем x ∈ (−∞ −3)∪(3; +∞). Данное множество полностью содержится в ОДЗ логарифма, значит это и есть ответ.
Преобразование логарифмических неравенств
Часто исходное неравенство отличается от приведенного выше. Это легко исправить по стандартным правилам работы с логарифмами - см. «Основные свойства логарифмов ». А именно:
- Любое число представимо в виде логарифма с заданным основанием;
- Сумму и разность логарифмов с одинаковыми основаниями можно заменить одним логарифмом.
Отдельно хочу напомнить про область допустимых значений. Поскольку в исходном неравенстве может быть несколько логарифмов, требуется найти ОДЗ каждого из них. Таким образом, общая схема решения логарифмических неравенств следующая:
- Найти ОДЗ каждого логарифма, входящего в неравенство;
- Свести неравенство к стандартному по формулам сложения и вычитания логарифмов;
- Решить полученное неравенство по схеме, приведенной выше.
Задача. Решите неравенство:
Найдем область определения (ОДЗ) первого логарифма:
Решаем методом интервалов. Находим нули числителя:
3x
− 2 = 0;
x
= 2/3.
Затем - нули знаменателя:
x
− 1 = 0;
x
= 1.
Отмечаем нули и знаки на координатной стреле:

Получаем x ∈ (−∞ 2/3)∪(1; +∞). У второго логарифма ОДЗ будет таким же. Не верите - можете проверить. Теперь преобразуем второй логарифм так, чтобы в основании стояла двойка:
Как видите, тройки в основании и перед логарифмом сократились. Получили два логарифма с одинаковым основанием. Складываем их:

log 2 (x
− 1) 2 < 2;
log 2 (x
− 1) 2 < log 2 2 2 .
Получили стандартное логарифмическое неравенство. Избавляемся от логарифмов по формуле. Поскольку в исходном неравенстве стоит знак «меньше», полученное рациональное выражение тоже должно быть меньше нуля. Имеем:
(f
(x
) − g
(x
)) · (k
(x
) − 1) < 0;
((x
− 1) 2 − 2 2)(2 − 1) < 0;
x
2 − 2x
+ 1 − 4 < 0;
x
2 − 2x
− 3 < 0;
(x
− 3)(x
+ 1) < 0;
x
∈ (−1; 3).
Получили два множества:
- ОДЗ: x ∈ (−∞ 2/3)∪(1; +∞);
- Кандидат на ответ: x ∈ (−1; 3).
Осталось пересечь эти множества - получим настоящий ответ:

Нас интересует пересечение множеств, поэтому выбираем интервалы, закрашенные на обоих стрелах. Получаем x ∈ (−1; 2/3)∪(1; 3) - все точки выколоты.
Логарифмические неравенства
На предыдущих уроках мы с вами познакомились с логарифмическими уравнениями и теперь знаем, что это такое и как их решать. А сегодняшний урок будет посвящен изучению логарифмических неравенств. Что же это за такие неравенства и в чем разница между решением логарифмического уравнения и неравенства?
Логарифмические неравенства - это неравенства, которые имеют переменную, стоящую под знаком логарифма или в его основании.
Или же, можно еще сказать, что логарифмическое неравенство – это такое неравенство, в котором его неизвестная величина, как и в логарифмическом уравнении, будет стоять под знаком логарифма.
Простейшие логарифмические неравенства имеют такой вид:
где f(x) и g(x) являются некоторыми выражениями, которые зависят от x.
Давайте это рассмотрим на таком примере: f(x)=1+2x+x2, g(x)=3x−1.
Решение логарифмических неравенств
Перед решением логарифмических неравенств, стоит отметить, что они при решении имеют сходство с показательными неравенствами, а именно:
Во-первых, при переходе от логарифмов к выражениям, стоящим под знаком логарифма, нам также необходимо сравнить основание логарифма с единицей;
Во-вторых, решая логарифмическое неравенство, используя замену переменных, нам необходимо решать неравенства относительно замены до того момента, пока мы не получим простейшее неравенство.
Но это мы с вами рассмотрели сходные моменты решения логарифмических неравенств. А сейчас обратим внимание на довольно таки существенное отличие. Нам с вами известно, что логарифмическая функция обладает ограниченной областью определения, поэтому переходя от логарифмов к выражениям, стоящим под знаком логарифма, нужно брать в расчет область допустимых значений (ОДЗ).
То есть, следует учитывать, что решая логарифмическое уравнение мы с вами, можем сначала находить корни уравнения, а потом делать проверку этого решения. А вот решить логарифмическое неравенство так не получится, поскольку переходя от логарифмов к выражениям, стоящим под знаком логарифма, необходимо будет записывать ОДЗ неравенства.
Вдобавок стоит запомнить, что теория неравенств состоит из действительных чисел, которыми являются положительные и отрицательные числа, а также и число 0.
Например, когда число «а» является положительным, то необходимо использовать такую запись: a >0. В этом случае, как сумма, так и произведение таких этих чисел также будут положительными.
Основным принципом решения неравенства является его замена на более простое неравенство, но главное, чтобы оно было равносильно данному. Дальше, также мы получили неравенство и снова его заменили на то, которое имеет более простой вид и т.д.
Решая неравенства с переменной нужно находить все его решения. Если два неравенства имеют одну переменную х, то такие неравенства равносильны, при условии, что их решения совпадают.
Выполняя задания на решение логарифмических неравенств, необходимо запомнить, что когда a > 1, то логарифмическая функция возрастает, а когда 0 < a < 1, то такая функция имеет свойство убывать. Эти свойства вам будут необходимы при решении логарифмических неравенств, поэтому вы их должны хорошо знать и помнить.
Способы решения логарифмических неравенств
Сейчас рассмотрим некоторые способы, которые имеют место при решении логарифмических неравенств. Для лучшего понимания и усвоения, попытаемся в них разобраться на конкретных примерах.
Нам с вами известно, что простейшее логарифмическое неравенство имеет такой вид:
В этом неравенстве V – является одним из таких знаков неравенства, как: <,>, ≤ или ≥.
Когда основание данного логарифма больше единицы (a>1), осуществляя переход от логарифмов к выражениям, стоящим под знаком логарифма, то в этом варианте знак неравенства сохраняется, и неравенство будет иметь такой вид:
что равносильно такой вот системе:

В случае же, когда основание логарифма больше нуля и меньше единицы (0 Это равносильно данной системе: Посмотрим еще примеры решения простейших логарифмических неравенств, приведенных на картинке ниже: Задание.
Давайте попробуем решить такое вот неравенство: Решение области допустимых значений. Теперь попробуем умножить его правую часть на: Смотрим, что у нас получится: Теперь, давайте с вами перейдем к преобразованию подлогарифмических выражений. В связи с тем, что основание логарифма 0< 1/4 <1, то от сюда следует, что знак неравенства изменится на противоположный: 3x - 8 > 16; А из этого следует, что интервал, который мы получили, целиком и полностью принадлежит ОДЗ и является решением такого неравенства. Вот какой ответ у нас получился: А теперь давайте попробуем проанализировать, что нам необходимо для успешного решения логарифмических неравенств? Во-первых, сосредоточить все свое внимание и постараться не допускать ошибок при выполнении преобразований, которые даны в этом неравенстве. Также, следует запомнить, что при решении таких неравенств нужно не допускать расширений и сужений ОДЗ неравенства, которые могут привести к потере или приобретению посторонних решений. Во-вторых, при решении логарифмических неравенств необходимо научиться мыслить логически и понимать разницу между такими понятиями, как система неравенств и совокупность неравенств, чтобы вы без проблем смогли осуществлять отбор решений неравенства, при этом руководствуясь его ОДЗ. В-третьих, для успешного решения таких неравенств каждый из вас должен отлично знать все свойства элементарных функций и четко понимать их смысл. К таким функциям относятся не только логарифмические, но и рациональные, степенные, тригонометрические и т.д., одним словом, все те, которые вы изучали на протяжении школьного обучения алгебры. Как видите, изучив тему о логарифмических неравенствах, в решении этих неравенств нет ничего сложного при условии, если вы будете внимательны и настойчивы в достижении поставленных целей. Чтобы в решении неравенств не возникало никаких проблем, нужно как можно больше тренироваться, решая различные задания и при этом запоминать основные способы решения таких неравенств и их систем. При неудачных решениях логарифмических неравенств, следует внимательно проанализировать свои ошибки, чтобы в будущем не возвращаться к ним снова. Для лучшего усвоения темы и закрепления пройденного материала, решите следующие неравенства: Определение логарифма
проще всего записать математически: Определение логарифма можно записать и другим способом: Обратите внимание на ограничения которые накладываются на основание логарифма (a
) и на подлогарифмическое выражение (x
). В дальнейшем эти условия превратятся в важные ограничения для ОДЗ, которые нужно будет учитывать при решении любого уравнения с логарифмами. Итак, теперь кроме стандартных условий приводящих к ограничениям на ОДЗ (положительность выражений под корнями четных степеней, не равенство знаменателя нолю и т.д.) нужно учитывать еще и следующие условия: Обратите внимание, что ни основание логарифма, ни подлогарифмическое выражение не могут быть равными нолю. Обратите также внимание и на то, что само значение логарифма может принимать все возможные значения, т.е. логарифм может быть положительным, отрицательным и равным нолю. У логарифмов есть очень много различных свойств, которые следуют из свойств степеней и определения логарифма. Перечислим их. Итак, свойства логарифмов: Логарифм произведения: Логарифм дроби: Вынесение степени за знак логарифма: Обратите особо пристальное внимание на те из последних перечисленных свойств, в которых появляется знак модуля после вынесения степени. Не забывайте, что при вынесении четной степени за знак логарифма, под логарифмом или в основании нужно оставить знак модуля.
Другие полезные свойства логарифмов: Последнее свойство очень часто применяется в сложных логарифмических уравнениях и неравенствах. Его нужно помнить также хорошо, как и все остальные, хотя о нём часто забывают. Самые простые логарифмические уравнения имеют вид: А их решение задаётся формулой, которая напрямую следует из определения логарифма: Другие простейшие логарифмические уравнения, это такие, которые с помощью алгебраических преобразований и приведённых выше формул и свойств логарифмов можно свести к виду: Решение таких уравнений с учетом ОДЗ выглядит следующим образом: Некоторые другие логарифмические уравнения с переменной в основании
могут быть сведены к виду: В таких логарифмических уравнениях общий вид решения также напрямую следует из определения логарифма. Только в этом случае имеются дополнительные ограничения для ОДЗ, которые нужно учесть. В итоге, для решения логарифмического уравнения с переменной в основании нужно решать следующую систему: При решении более сложных логарифмических уравнений, которые нельзя свести к одному из представленных выше уравнений, также активно применяется метод замены переменных
. Как обычно, применяя этот метод нужно помнить, что после введения замены уравнение должно упроститься и больше не содержать старой неизвестной. Также нужно не забывать выполнять обратную замену переменных. Иногда при решении логарифмических уравнений приходится также использовать графический метод
. Данный метод состоит в том, чтобы как можно более точно построить на одной координатной плоскости графики функций, которые стоят в левой и правой частях уравнения, а затем найти координаты точек их пересечения по чертежу. Полученные таким образом корни обязательно нужно проверить подстановкой в первоначальное уравнение. При решении логарифмических уравнений часто также бывает полезен метод группировки
. При использовании этого метода главное помнить, что: для того чтобы произведение нескольких множителей было равно нолю, необходимо, чтобы хотя бы один их них равнялся нолю, а остальные существовали
. Когда множителями являются логарифмы или скобки с логарифмами, а не просто скобки с переменными как в рациональных уравнениях, то может возникнуть много ошибок. Так как у логарифмов есть много ограничений на ту область, где они существуют. При решении систем логарифмических уравнений
чаще всего приходится использовать либо метод подстановки, либо метод замены переменных. Если есть такая возможность, то при решении систем логарифмических уравнений нужно стремиться к тому, чтобы каждое из уравнений системы по-отдельности привести к такому виду, при котором можно будет осуществить переход от логарифмического уравнения к рациональному. Простейшие логарифмические неравенства решаются примерно также как и аналогичные уравнения. Сначала, с помощью алгебраических преобразований и свойств логарифмов, их нужно постараться привести к такому виду, где у логарифмов в левой и правой части неравенства будут одинаковые основания, т.е. получить неравенство вида: После чего нужно перейти к рациональному неравенству, учитывая, что этот переход должен быть выполнен следующим образом: если основание логарифма больше единицы, то знак неравенства менять не нужно, а если основание логарифма меньше единицы, то нужно поменять знак неравенства на противоположный
(это значит поменять "меньше" на "больше" или наоборот). При этом знаки минус на плюс, в обход ранее изученных правил нигде менять не нужно. Запишем математически то, что получим в результате выполнения такого перехода. В случае если основание больше единицы получим: В случае если основание логарифма меньше единицы поменяем знак неравенства и получим следующую систему: Как видим при решении логарифмических неравенств как обычно учитывается также и ОДЗ (это третье условие в системах выше). Причем в этом случае есть возможность не требовать положительности обоих подлогарифмических выражений, а достаточно потребовать положительности только меньшего из них. При решении логарифмических неравенств с переменной в основании
логарифма необходимо самостоятельно рассматривать оба варианта (когда основание меньше единицы, и больше единицы) и объединять решения этих случаев в совокупность. При этом нужно не забывать и про ОДЗ, т.е. про то, что и основание и все подлогарифмические выражение должны быть положительными. Таким образом, при решении неравенства вида: Получим следующую совокупность систем: Более сложные логарифмические неравенства могут также решаться с помощью замены переменных. Некоторые другие логарифмические неравенства (как и логарифмические уравнения) для решения требуют проведения процедуры логарифмирования обоих частей неравенства или уравнения по одинаковому основанию. Так вот при проведении такой процедуры с логарифмическим неравенствами имеется тонкость. Обратите внимание, что при логарифмировании по основанию большему единицы, знак неравенства не изменяется, а если основание меньше единицы, то знак неравенства изменяется на противоположный. Если логарифмическое неравенство не может быть сведено к рациональному или решено с помощью замены, то в этом случае нужно применять обобщенный метод интервалов
, который состоит в следующем: Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия: Успешное, старательное и ответственное выполнение этих трех пунктов позволит Вам показать на ЦТ отличный результат, максимальный из того на что Вы способны. Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на почту. Написать об ошибке можно также в социальной сети (). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка. Цели урока: Дидактические:
Развивающие:
развивать память, внимание, логическое мышление, навыки
сравнения, уметь обобщать и делать выводы Воспитательные:
воспитывать аккуратность, ответственность за
выполняемое задание, взаимопомощь. Методы обучения:
словесный,
наглядный,
практический,
частично-поисковый,
самоуправления,
контроля. Формы организации познавательной деятельности учащихся:
фронтальный,
индивидуальный,
работа в парах. Оборудование:
набор тестовых заданий, опорный конспект, чистые
листы для решений. Тип урока:
изучение нового материала. Ход урока 1. Организационный момент.
Объявляются тема и цели урока, схема
проведения урока: каждому ученику выдается оценочный лист, который ученик
заполняет в течении урока; для каждой пары учеников – печатные материалы с
заданиями, выполнять задания нужно в парах; чистые листы для решений; опорные
листы: определение логарифма; график логарифмической функции, ее свойства;
свойства логарифмов; алгоритм решения логарифмических неравенств. Все решения после самооценки сдаются учителю. Оценочный лист учащегося 2. Актуализация знаний.
Указания учителя. Вспомните определение логарифма, график логарифмической
функции и ее свойства. Для этого прочитайте текст на с.88–90, 98–101 учебника
“Алгебра и начала анализа 10–11” под редакцией Ш.А Алимова, Ю.М Колягина и др. Ученикам раздаются листы, на которых записаны: определение логарифма;
изображен график логарифмической функции, ее свойства; свойства логарифмов;
алгоритм решения логарифмических неравенств, пример решения логарифмического
неравенства, сводящегося к квадратному. 3. Изучение нового материала.
Решение логарифмических неравенств основано на монотонности логарифмической
функции. Алгоритм решения логарифмических неравенств: А) Найти область определения неравенства (подлогарифмическое выражение больше
нуля). Учебный элемент № 1. Цель: закрепить решение простейших логарифмических неравенств Форма организации познавательной деятельности учащихся: индивидуальная
работа. Задания для самостоятельной работы на 10 минут. Для каждого неравенства
имеются несколько вариантов ответов, нужно выбрать верный и проверить по ключу. Учебный элемент № 2. Цель: закрепить решение логарифмических неравенств, применяя свойства
логарифмов. Указания учителя. Вспомните основные свойства логарифмов. Для этого
прочитайте текст учебника на с.92, 103–104. Задания для самостоятельной работы на 10 минут. КЛЮЧ: 2113, максимальное кол-во баллов – 8 б. Учебный элемент № 3. Цель: изучить решение логарифмических неравенств методом сведения к
квадратному. Указания учителя: метод сведения неравенства к квадратному состоит в том,
что нужно преобразовать неравенство к такому виду, чтобы некоторую
логарифмическую функцию обозначить новой переменной, получив при этом квадратное
неравенство относительно этой переменной. Применим метод интервалов. Вы прошли первый уровень усвоения материала. Теперь вам придется
самостоятельно выбрать метод решения логарифмических уравнений, используя все
свои знания и возможности. Учебный элемент № 4. Цель: закрепить решение логарифмических неравенств, выбрав самостоятельно
рациональный способ решения. Задания для самостоятельной работы на 10 минут Учебный элемент № 5. Указания учителя. Молодцы! Вы освоили решение уравнений второго уровня
сложности. Целью дальнейшей вашей работы является применение своих знаний и
умений в более сложных и нестандартных ситуациях. Задания для самостоятельного решения: Указания учителя. Замечательно, если вы справились со всем заданием.
Молодцы! Оценка за весь урок зависит от числа набранных баллов по всем учебным
элементам: Оценочные лисы сдать учителю. 5. Домашнее задание: если вы набрали не более 15 б – выполните работу над
ошибками (решения можно взять у учителя), если вы набрали более 15 б – выполните
творческое задание по теме “Логарифмические неравенства”.

Решение примеров
![]()



3x > 24;
х > 8.![]()
Что необходимо для решения логарифмических неравенств?
Домашнее задание




![]()
![]()

![]()

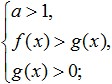

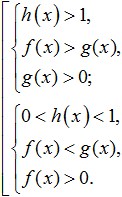
Как успешно подготовиться к ЦТ по физике и математике?
Нашли ошибку?
Б) Представить (если возможно) левую и правую части неравенства в виде
логарифмов по одному и тому же основанию.
В) Определить, возрастающей или убывающей является логарифмическая функция: если
t>1, то возрастающая; если 0
Г) Перейти к более простому неравенству (подлогарифмических выражений),
учитывая, что знак неравенства сохранится, если функция возрастает, и изменится,
если она убывает.
КЛЮЧ: 13321, максимальное кол-во баллов – 6 б.














